中央値と四分位数範囲について

✅中央値と平均値の使い分け

正規分布であれば平均値と標準偏差を用いてきたが、正規分布ではない、左右非対称のデータがある場合はどうしたら良いのか。平均値ではなく中央値を用いる。

平均値はたった１つの巨大な外れ値があった場合に、平均値が大きく動いてしまう。しかし中央値であれば大きな外れ値があってもずれない（中央値のほうが安定しているとも言える）。

→よって、正規分布でないデータや正規分布かどうかわからないデータの場合では平均値よりも中央値を使ったほうが良い。

✅標準偏差と四分位範囲（Inter Quartile Range,IQR)の使い分け

四分位範囲は名前の通り、データを４つに分ける。

↓クラスAとクラスBの点数を高い順に並べた一例

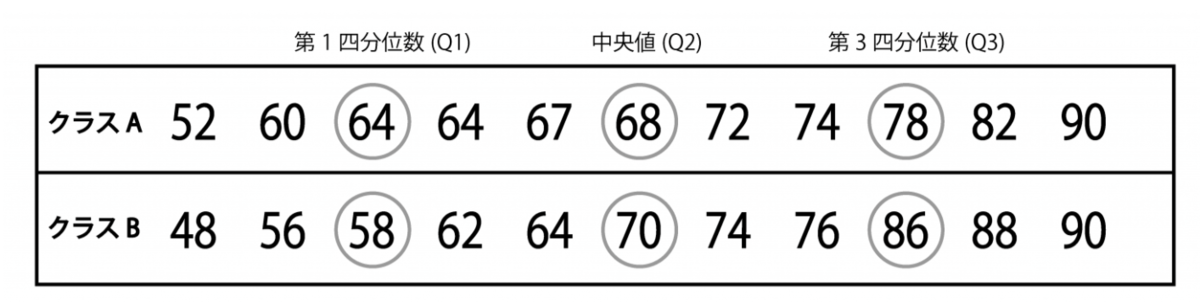
中央値がデータを小さい順に並べたときにど真ん中になる数字であったのに対して、四分位範囲はデータを４当分する。

最小データと中央値の間の数字が第１四分位数で、中央値と最大値の間の数字が第３四分位数になる。中央値は第２四分位数ともいう。

四分位範囲とは第一４分位数から第３四分位数の間の範囲の数字のこと。全体の５０％が四分位範囲に含まれる。なお、IQR/2を四分位偏差と呼ぶ。

★データが偶数の場合：

上述の例はデータの数が奇数であった。もしクラスが１０人の場合はどのように四分位範囲を計算するのか。データが偶数の場合は数の大きいグループと数の小さいグループの２つに分ける。それぞれのグループで中央値を算出し、それぞれの中央値がそれぞれ第１四分位数、第３四分位数になる。